it’s about time.

11/10/2014

The concept of time is something that people have written about since the beginning of time (sorry, I know that’s awkward to read). Time with regard to engine management systems and fuel injection isn’t something people really give too much thought to, though. I thought it would be nice to break down how important time is with fuel injection and engine management (we’ll just mainly focus on fuel injection time in this article.)

Combustion events happen pretty quickly, even with arguably boring engines, like the one in your mom’s mini-van. The point and purpose of this article is to show you how fast these event happen and why that matters to you and your injector choice.

The basics of port fuel injectors are pretty simple:

– (part 1) You have an injector that will flow a given amount of volume of fuel per minute. (Most know this is lb/hour, or cc/min).

– (part 2) The injector can flow during the entire two crankshaft revolution engine cycle. (Remember that a 4-stroke engine requires two complete revolutions to complete an engine cycle). If the injector is open during this entire time, this is represented as 100% Injector Duty Cycle (or 100% IDC).

100% IDC should be avoided at all costs. Bad things can happen to the injector at IDC above 95%. A safe place to
wind up is around 85% max.

– (part 3) This engine cycle time calculation is really easy to do.

Part 1:
If you buy a set of injectors from whom ever (but let’s be honest, you really should buy injectors from ID www.injectordynamics.com *end of shameless plug*), they will come with a flow rating, 1000cc/min, 500lb/hour, etc. What that means is that a 1000cc / min injector can flow 1000 cubic centimeters of fuel in one minute. The neat thing about that is that pretty much all injectors have a linear flow relationship above 2 milliseconds of ON time. Let’s take an example:

You have an injector that flows 60 pounds of fuel per hour (630cc per minute for you metric folks). If you divide 60 pounds of fuel per hour by 60 minutes you will get 1 pound of fuel per minute.

If you know that you need 0.6 lbs of fuel per minute to achieve a certain air fuel ratio, at a certain rpm (say 8000). you can easily derive from that that you will have to operate at 60% duty cycle to flow 0.6 lbs of fuel per minute.

Sidenote: There are really sweet equations to determine air flow based off of some standards and some values like displacement, VE, fuel type, and some others. If there are enough people interested I’ll walk through the entire process. It’s neat but it’s lengthy! You can actually calculate that required fuel per minute that is listed above (0.6 lbs of fuel per minute).

Part 2:
A 4 stroke engine cycle is exactly that, 4 individual events that must occur in sequential order to complete one engine cycle.

Intake stroke (as the piston travels down)
Compression stroke (as the piston travels back up)
Power stroke (as the piston travels back down after the explosion)
Exhaust stroke (as the piston travels back up to expel the exhaust gases).

On a port fuel injection car, the fuel injector is behind the intake valve and therefore, the fuel allowed to enter the engine is really ultimately controlled by the intake valve position. The fuel injector can stay open for the entire engine cycle (all 4 strokes) and fuel will only travel in to the cylinder to be ignited when the intake valve is open. If it’s on for the entire engine cycle, this represents 100% injector duty cycle.

Sidenote: Direct injection is now in a number of cars and this principal is completely different, as the injector nozzle is DIRECTLY (see what I did there?) in the combustion chamber. The maximum duty cycle that they can operate at is around 50%. Direct injection is pretty neat to think about considering the duty cycle limitations, the 400-3000 psi fuel pressure ranges, and the fact that the OE ECU’s are controlling multiple injections per cycle depending on load and engine speed, wild.

Part 3:
So, we learned in part 1 that we have an imaginary engine that needs 0.6 lbs of fuel per minute to achieve a certain air fuel ratio (or AFR) at 8000 rpm, and that this will require 60% injector duty cycle to do so based on using a 60 lb per minute injector.

That doesn’t really even mean a whole lot unless you can tell the fuel injector how long to stay on for. 60% IDC doesn’t really mean a whole lot to an ECU. It does in some cases, but not really with injectors. So, let’s figure out how much time exactly 60% IDC means, or more specifically, how much time exactly does the injector need to be open for.

Lets say our engine is at 8000 RPM. We want to figure out how much time one engine cycle takes (4 strokes).

We first need to take the engine speed and divide it by 2 to get the number cycles. The 2 is there because it takes 2 revolutions to make one engine cycle.

8000 / 2 = 4000 engine cycles per minute.

Then we want to figure out the number of cycles per second. So we’ll divide the cycles per minute by 60 seconds to find out the cycles per second.

4000 / 60 = 66.66 cycles per second. (pretty wild if you think about it, right?)

Then we want to figure out the time it takes for each engine cycle. So we can just divide 1 by the number of cycles per second.

1 / 66.66 = 0.015 seconds per cycle. This equates to 15 milliseconds per cycle.

So now we know how long it takes for each cycle at 8000 rpm. So we know from above that our imaginary engine needs 0.6 lb/min of fuel to obtain our target AFR at 8000 rpm, and we know that it will require 60% duty cycle to flow 0.6 lb/min with a 60 lb/hour fuel injector.

So now it’s easy! We just need to multiply the time that the engine cycle takes by the duty cycle (divided by 100)

(15 ms * (60/100)) = 9 milliseconds

Are you still reading? I hope you’re not more confused than when you started.

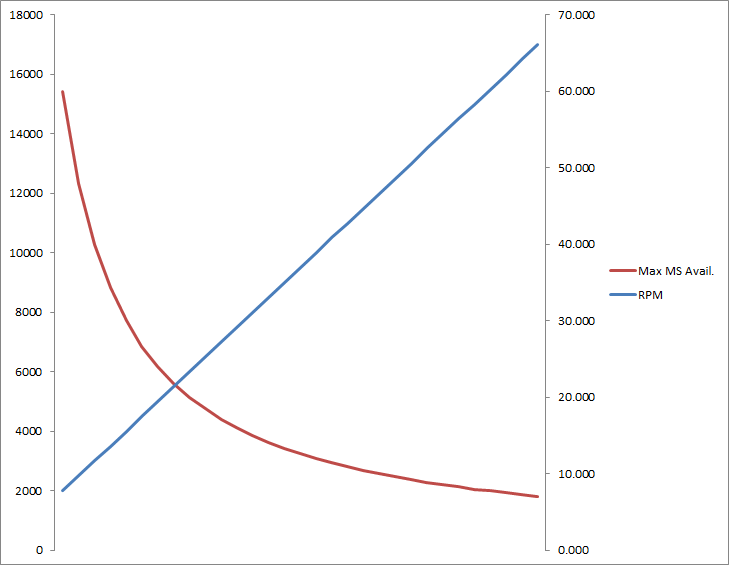
So I don’t get accused (again) of creating a boring looking wall of text, here’s a graph showing engine cycle time vs. RPM.

Here’s a fun fact to end it with. Moto GP bikes have rev limiters around 17,500-18,000 RPM. If you calculate it out, at 18,000 rpm, that engine completes two revolutions in 6.6 milliseconds. That’s 0.006 seconds! Whoa.