Blog

Tag Archives: gps



logo

Recent Posts

Aug. 03, 2021

INS or IMU? It depends.

sander , , , Leave a comment

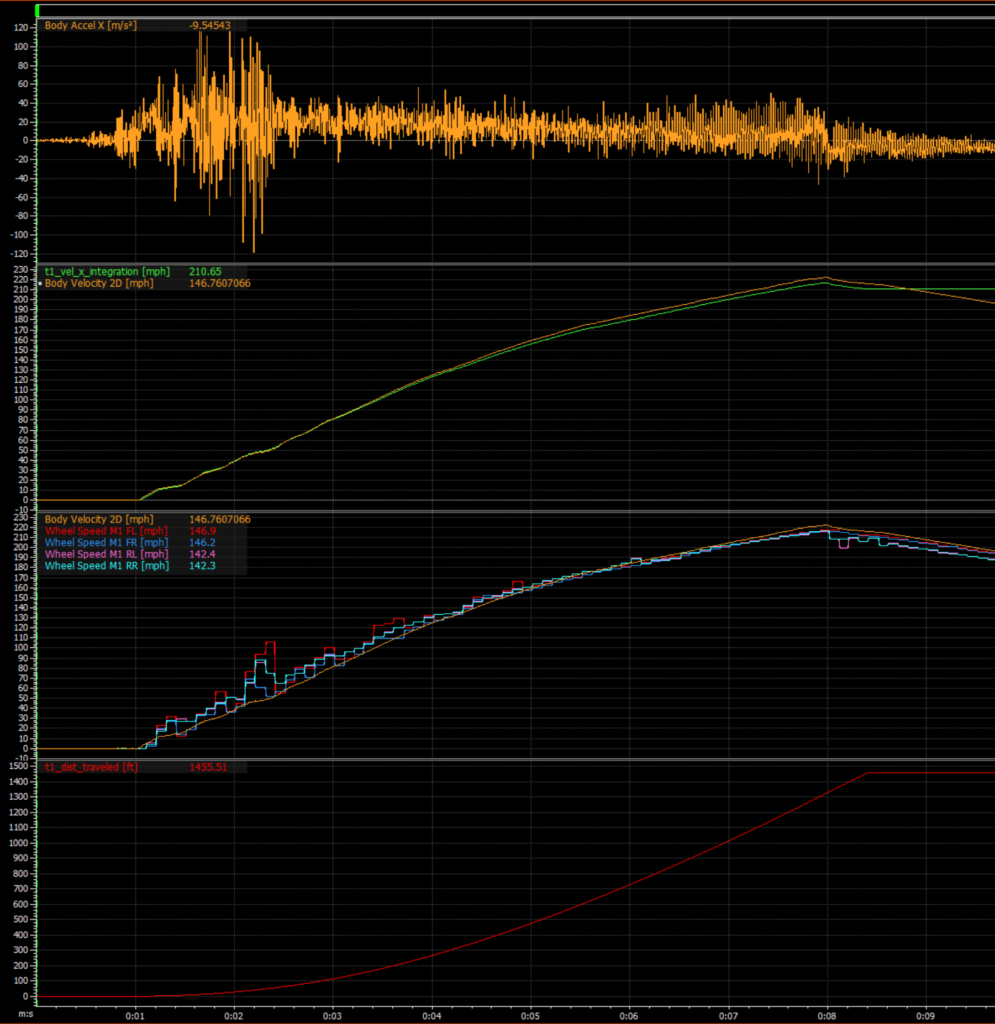
It depends how long it takes you to do what ever you’re trying to do.

There. That’s the end of the article.

Just kidding.

A Terminology Tangent

First, you’re probably thinking, “Tangent? This guy hasn’t even started writing anything yet“.

Second, I probably should apologize for having two products, that look nearly identical, that have nearly the same name, targeted at different applications, and with wildly different price tags. I am trying to take the Ron Swanson approach to making products. I’d like to just call things what they are. No marketing, no flair, no sponsored product placements. So, anyway, let me take a second and remind you, my loyal readership, what these acronyms stand for:

INS stands for Inertial Navigation System. This is an industry term in robotics that, generally speaking, defines a system that is a GNSS receiver, accelerometer, gyroscope, barometer, and temperature sensor (among other sensors, sometimes) combined together with a complex sensor fusion algorithm to produce a single high-rate, high-accuracy 6DOF pose (and corresponding derivatives that we will talk about later in this post).

sidenote_1: 6DOF Pose stands for 6 Degree Of Freedom Pose. These 6 individual degrees of freedom are: Roll, Pitch, Yaw, X Position, Y Position, Z Position. When combined, they represent the position of the sensor in a 3D world.

IMU stands for Inertial Measurement Unit. This term is a bit more complicated. This is also an industry term (in robotics, and motorsport at the sub-pro level) that, generally speaking, defines way way too many different sensors, systems, and products.

In motorsport, an IMU is generally defined as a sensor that will give you acceleration, and angular velocity. It is generally a very basic raw sensor output with no sensor fusion or on-board math going on.

In robotics, an IMU is generally defined as an accelerometer, gyroscope, barometer, and temperature sensor combined together with a complex sensor fusion algorithm to produce high-rate / high-accuracy orientation (roll, pitch, yaw), acceleration, and angular velocity.

INS on the left, IMU on the right
The PPIHC Open Class champion that I was able to use as a test platform to benchmark some new INS and IMU beta features

So, as you can probably tell at this point, I’m following the terminology of the robotics world in naming these two products. The robotics definition of the INS is what the Obsidian Motorsport Group INS is. The same is true for the Obsidian Motorsport Group IMU.

Derivatives and Antiderivatives

I know, scary math word, but please relax. I’m going to do everything in my power to use intuitive examples to demonstrate some things about how the IMU (and to some extent, at a very basic level, the INS) derive some of their more interesting data products.

Derivatives are simply the representation of the change of something divided by the time it took to make that change. Antiderivatives (also referred to as Integration) are the opposite. Stay with me here, practical examples that are not your run of the mill “passenger on a train” physics examples are incoming…

Lets assume that you have a general purpose 3-axis accelerometer mounted in a vehicle, rigidly attached to the chassis, and the X-axis is pointed forward, the Y-axis is pointed left, and the Z-axis is pointed up.

sidenote_02: This accelerometer mounting mentioned above (and our INS / IMU…) follows a “Right-Hand Rule” convention. If you curl your right hand in to a fist and rotate it such that your thumb is up, and do the following:

  • Point your pointer finger forward
  • Point your middle finger toward the left
  • Point your thumb in the air

Your pointer finger will be the X-axis, your middle finger will be the Y-axis, and your thumb will be the Z-axis. No matter how you mount a “Right-Hand Rule” IMU, if you keep the finger-to-axis assignments the same, you’ll be able to envision what the coordinate frame looks like with your hand! Neat.

Using the coordinate reference frame mentioned above, when the vehicle travels forward, there will be positive acceleration present in the X-axis.

  • If you integrate the acceleration (using units of m/s/s) in the X-axis, you will get velocity (using units m/s) in the X-axis.
  • If you integrate the velocity (using units of m/s) in the X-axis, you will get position (using units of m) in the X-axis.

The picture below should illustrate that point well.

  • The blue trace at the top is a measure of longitudinal acceleration (forward + / backward – ) in units of m/s/s.
  • The green trace is a measure of longitudinal velocity in units of m/s. This is a result of integration of the blue trace.
  • The red trace is a measure of longitudinal position in units of m. This is a result of integration of the green trace.
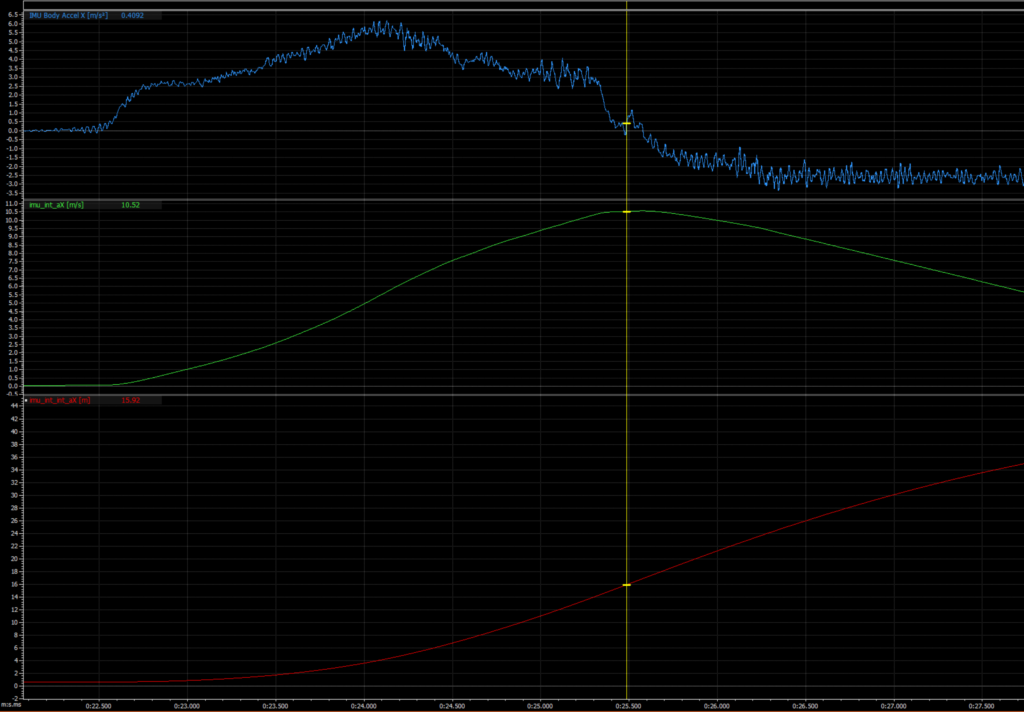
Acceleration (top), Velocity (middle), Position (lower)

sidenote_04: It’s important to remember that there are a lot of factors that go in to creating an accurate acceleration measurement to do these integrations off of. You should absolutely try this on your own with whatever sensor you want to use, but be warned, It’s harder than you think to do this with a basic accelerometer.

So, now you know the relationship of acceleration, velocity, and position. I feel pretty strongly that this is an important concept to grasp to discuss the next part of this post…

Error

Now that we know how integration works, intuitively anyway, we can talk about the biggest issue with integration: error.

Accelerometers are not perfect instruments. Even the fanciest ones on the planet are prone to small error based on a multitude of factors (Namely temperature for the ones that normal civilians have access to). When we integrate acceleration to get velocity, any small error in acceleration, will propagate forward as an error in velocity. This is compounded when we integrate velocity to get position!

The picture below, should illustrate that point well. It is the same data as the trace above, but with some error introduced in the longitudinal acceleration measurement. Check out the position error at the end, it’s ~40m !

  • The purple trace at the top is “nearly” the same acceleration as the IMU Body Accel X [m/s/s] channel.
  • The purple trace in the middle is a result of integration of the purple acceleration measurement at the top. Notice the significant error (~4 m/s).
  • The purple trace at the bottom is a result of integration of the purple velocity trace in the middle. Notice the massive error (~40m).
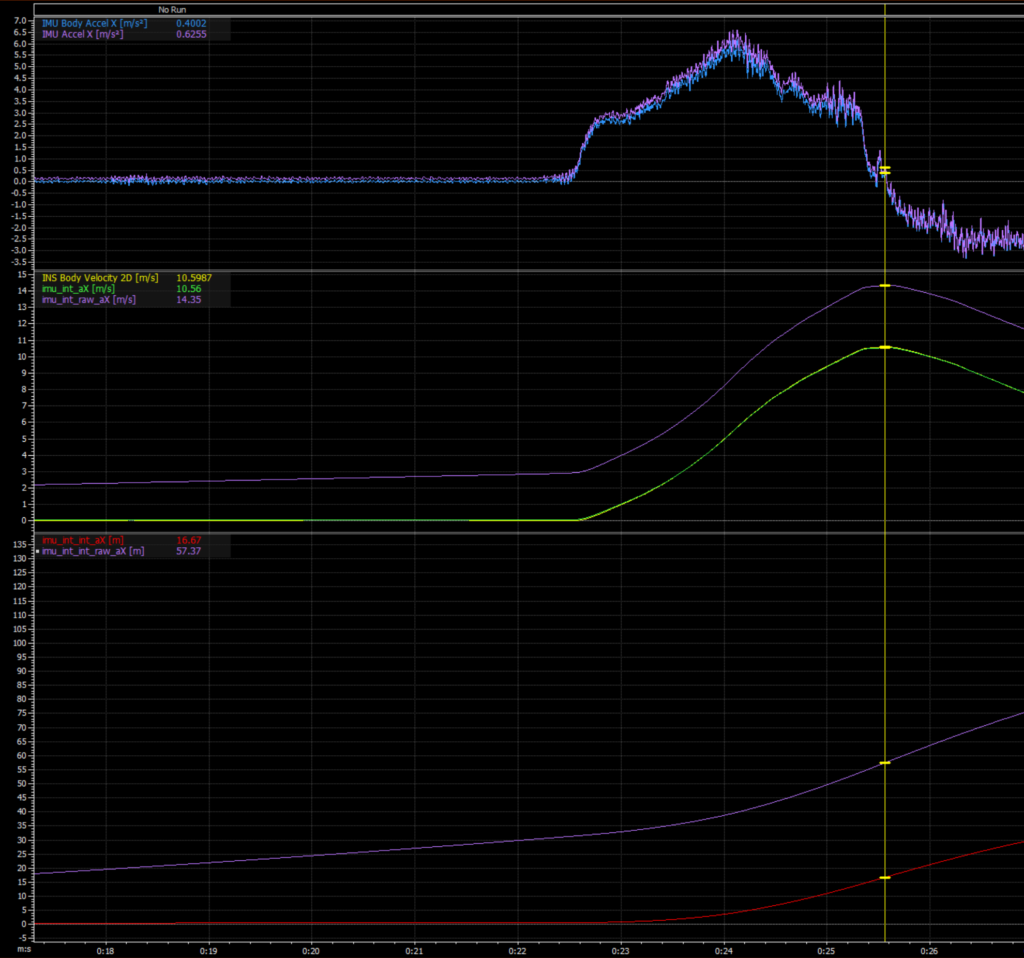
The two acceleration channels don’t look that different, do they…

Our IMU goes through a factory calibration at the chip level, then a second calibration (at our office) to try to do our best to remove any errors that are introduced after installation (soldering). We spend a lot of time with this to try to give you acceleration data that is in blue, and not in purple.

In addition to our calibration processes, there are online algorithms that are running that are constantly (on the sensor itself) trying to estimate and correct any errors in the acceleration and gyroscope measurements to make sure that we’re providing you the best data possible. However, since those algorithms have no real understanding about how the vehicle is moving through the world (say, with a GNSS / GPS receiver like the INS…), these bias correction algorithms are only effective to a point. This “point” is about 30-45 seconds after the vehicle has left the starting line and the integration process has begun.

Do I need an INS or can I use an IMU? TELL ME, SANDER.

Okay, okay. I hear you.

The IMU is explicitly designed for standing start, ground vehicle, racing that lasts for less than 30-45 seconds.

The INS is explicitly designed for everything. Since the sensor has a GNSS / GPS receiver on board, the sensor can automatically mitigate biases that creep in over time to the accelerometer and gyroscope. It has no time bound.

The IMU will provide the following data products at up to 800hz:

  • Ground Speed*
  • Raw Acceleration (X, Y, Z)
  • Body Frame Acceleration (X, Y, Z)
  • Angular Velocity (X, Y, Z)
  • Orientation (Roll, Pitch, Yaw)

*The IMU will need to be sent a simple CAN message to tell it that the pass has started to generate Ground Speed. It’s easy to do, I promise.

The IMU will have the following features:

  • Adjustable baud rate (1mbps default, 500kbps, 250kbps)
  • Adjustable transmission rate (800hz, 400hz, 200hz, 100hz, 50hz, 25hz, 10hz).
  • Adjustable user tunable filters for acceleration / gyroscope data
  • Advanced Kalman filter tuning parameters

The sensor will be sold for $1750 and I will have a number in hand to sell in about 3-4 weeks. As always, if you have any questions, please email me at sander 4T obsidianeng d0t com

Now, you may be thinking, “Sander, you could have lead with that and I wouldn’t have had to read this stuff about derivatives, integration, and error propagation.”

You’re right. I could have.

Dec. 23, 2020

GPS? IMU? INS? What on Earth even is that?

sander , , Leave a comment

See what I did there?

I should start out by saying it’s been quite a while since I’ve written anything in a “blog” type format, so please be patient if I go off on a long tangent about something that’s powerfully uninteresting to you, my loyal readership.

Since my last post on this blog, I moved to California (San Francisco, specifically), got hit by yet another car while riding my bike, ate many delicious meals in San Francisco, had many successes with work, learned many hard lessons about living in a city, learned many more hard lessons about working with OE manufacturers on engineering projects, and (more relevant to this post) using / understanding / configuring / and making sense of Inertial GPS systems. Let’s go over some basics about the latter.

GPS / GNSS:

Many moons ago, I thought that when you placed a GNSS receiver / antenna on the roof of a race car, you could power it on, science would happen, and then it would tell you where on the earth you were. Magic.

I didn’t spend much time thinking about how it worked, because, well, it worked fine. It provided a nice visualization of where a car was on track. Fine. Great.

Over the past few years it has become increasingly obvious that it’s really important to understand how something works if you’re going to rely on the data it produces. A lot of the projects that I have been involved with over the past few years at some point rely on GNSS. It’s really important to know when to rely on it, when not to rely on it, and why.

sidenote_1: Sander, you keep writing “GNSS”, what does that even mean? “GNSS” stands for Global Navigation Satellite System. Some people often say “GPS” when they actually mean “GNSS”. You could plausibly argue that GNSS and GPS are interchangeable as ways to describe a system that can calculate where you are on the earth, but I felt it was worth mentioning that. GPS is actually a constellation (series of satellites in a specific orbit around the earth) of satellites that are owned and operated by the US Space Force. Yes, that Space Force. There are other constellations that are run by other countries such as “Galileo” (EU), “Beidou” (CN), “Glonass” (RU), “IRNSS” (India), “QZSS” (Japan). A GNSS system may use signals from satellites from one or more of these constellations to calculate your position on the globe. Neat right?

So, this begs the question: How do GNSS systems determine your position? How does it work? SANDER, TELL ME HOW SCIENCE HAPPENS!

sidenote_2: I’m going to do a super high level description of how things work, but if you’re interested in much more detail, you should really checkout this GPS Compendium (by u-Blox AG). It is a treasure trove of information about GNSS systems.

Basic things to know:

  • There are a number of satellites (in different constellations, run by different countries) orbiting the earth in a known trajectory / orbit.
  • Each satellite has an atomic clock on board to keep accurate time.
  • Atomic clocks are cool because they keep very accurate time for a very long time. (Not like your calculator wrist watch that you’re wearing right now. yes, you.)
  • Satellites regularly transmit their time so that GNSS receivers on the ground can receive this information.
  • If you take in a known position of the satellite, time from the satellite, you can use the speed of light as a constant to determine the distance from the GNSS receiver to the satellite.
  • You can determine a 3D position and time error with a minimum of 4 satellites. (Latitude, Longitude, Altitude, delta T error).
  • There are many sources of error that can cause accuracy issues (ionosphere time delay, multi-path signal errors, and other things outside the scope of this post)
  • The rate in which data is sent from these satellites will limit the rate at which we can calculate our position on the ground

That last bullet point is really the key issue here. Even very very expensive GNSS systems (NovAtel et. others) can not generate high frequency position measurements (lots of position updates every second) with just GNSS data alone. You need more data to help “fill in the gaps” between GNSS position updates. Well, how on earth would we “fill in the gaps”???

IMU (Inertial Measurement Unit):

IMU’s are generally understood to consist of a 3-axis accelerometer and a 3-axis gyroscope. What even is that? Let’s start with the accelerometer.

IMU (Accelerometer):

Like the name implies, the accelerometer measures acceleration. Now, you may be thinking, “Wow, Sander, you’re blowing my mind right now”. Or, maybe you’re not thinking that, hard to say.

I know that’s inherently obvious based on the name, but another way to think about acceleration measurement is that there is always acceleration to be measured (at least on our planet) by way of gravity. If you set a 3-axis accelerometer on a flat table, you will notice that the axis that is pointing up will report approximately 9.81 meters / second / second of “acceleration”. This is the measurement of gravity acting upon the table to keep it from floating away.

What can we do with an accelerometer beyond all of the well meaning, but painfully over simplified, statements about “my car pulled 3g’s off the line” or “I saw 2.5 lat G in T5 at Summit Point”? We can use calculus! From acceleration we can determine velocity doing a single integration, and we can determine relative position doing a double integration!

sidenote_3: I’m intentionally skipping an entire large chunk of explanation about removing gravity from acceleration measurements to actually get something useful from them and before integration to achieve velocity measurements, and entirely skipping bias calculation / error sources, for now.

This example shows live data from our INS (Body Accel X [m/s/s] and Body Velocity 2D [mph]). It also shows that you can integrate the Body Accel X [m/s/s] data and return velocity in the X axis ( t1_vel_x_integration [mph] ), and even distance traveled ( t1_dist_traveled [ft] )!

sidenote_4: Live distance traveled channels are being prototyped now and will be added to the sensor firmware later in 2021.

IMU (Gyroscope):

Like the name implies, the gyroscope measures gyroation. (Sorry, this is wildly incorrect, I just thought it would be funny at the time of writing relative to my previous bit about accelerometers measuring acceleration).

Gyroscopes measure the angular velocity about an axis. A simple way to think about this is if you placed a gyroscope on your hipster friends turntable (ya know, for vinyl records), and turned it on, the axis that is pointing straight up will probably indicate ~200 deg/second (33.3 RPM for 12″ records). This is simply measuring the speed at which the turntable is spinning.

What can we do with a gyroscope beyond making your friend with the turntable nervous by telling him it’s actually spinning at 198 deg/second as opposed to the 199.7999999999999999 deg/second it should be? You guessed it, more calculus! From angular rate we can determine the relative angles (more simply put, relative roll, pitch, and yaw) doing a single integration!

sidenote_5: It’s important to remember that in a rigid body (something that doesn’t flex or distort about the axis in which you’re measuring), the angular velocity (and resulting angle after integration) will be the same no matter where you place the gyroscope on the rigid body. Another way to think about this is simply that if you have a motorcycle that does a wheelie, no matter where you mount a gyroscope, the resulting pitch angle after integrating the pitch rate will be the same. 

This example shows live data from our INS on all channels.

sidenote_6: The pure_relative_pitch [deg] channel has a simple subtraction function to compensate for the mounting of the sensor in the vehicle. The live pitch measurement from the sensor will be absolute pitch (relative to gravity vector).

IMU (Error):

IMU’s are great because they can be light and small and provide very high rate data (1khz +), but it is also important to remember that they can be subject to long term integration error. These errors are omnipresent in in all IMU’s but especially ones that us common folk (read: not military) are allowed to buy.

Cheap IMU’s (less than a $10,000.00 or so) are usually Micro Electrical Mechanical System (MEMS) based units. They’re great because they’re small, cheap, light weight, and low power. But they are prone to massive error (usually mainly based around temperature, but there are other sources of error, too) if doing numerical integration over long time windows.

sidenote_7: “…long time windows” are definitely relative. Many consumer grade sensors (cheap) can even start showing integration error in seconds! On the flip side, many tactical grade (usually military only and > $10,000) will measure their integration error in hours)

These errors are tough to calibrate out, and are better addressed if you have another reference to compare your velocity and position to, periodically.

INS (Inertial Navigation System):

Here are some things we now understand:

  • GNSS systems can be highly accurate, but the rate at which they can provide position updates is relatively slow.
  • IMU’s can provide very fast measurements from which you can determine position, velocity, and orientation. However, their accuracy can become quite poor very quickly when doing single (or double) integrations.

An Inertial Navigation System (INS), combines these two sensors and uses the global accuracy of a GNSS system and the speed of an IMU! These INS systems use some derivative of a Kalman Filter (non-linear Extended or Unscented) to combine these sensor inputs perform what is sometimes called “Sensor Fusion” to generate one smooth cohesive output.

sidenote_8: Kalman Filters are a constant source of interest and wonder, however I think explaining how they work is outside of the scope of this blog post.

What is the point of this wall of text:

Well, I have put together an Inertial GPS system that I would like to sell. I am simply calling an INS. It uses a tried and true Extended Kalman Filter that is very robust and platform (or motion model) agnostic (car, motorcycle, plane, rally-car (read: plane)). I have tried really hard to make integrating this sensor as easy as is humanly possible to any modern, high-end data analysis / control system.

Here are the features:

  • 400Hz 32-bit Position (Latitude, Longitude, Altitude)
  • 400Hz 32-bit Velocity (Body X, Body Y, Body Z, and 2D Speed)
  • 400Hz 32-bit Body Frame Acceleration (Gravity Removed) (X, Y, Z) with online acceleration bias compensation
  • 400Hz 32-bit Angular Rate (X, Y, Z) with online gyro bias compensation
  • 400Hz 16-bit Orientation (Roll, Pitch, Yaw (Degrees))
  • 100Hz “MoTeC GPS” simulation option for integration with MoTeC M1 ECU applications with locked firmware (GT-R, Lamborghini, etc…)
  • CAN (1mbps) Output
  • Extensive integration support (MoTeC Dash Config, MoTeC M1 Build Project Module, DBC file)
  • CNC aluminum enclosure with Deutsch ASL connection and optional IP68 sealing
  • Custom firmware available for customer specific addressing, precision, transmit rates, conversions, units, additional on-board math channels, etc…

On the www.obsidianeng.com/downloads page you will find manuals, DBC files, MoTeC dash configuration files, and MoTeC M1 Build Modules.

The sensors will be available for purchase in Q1 2021. The cost will be $4500.00. Please shoot me an email (sander at_sign obsidianeng.com) with more questions.