Blog

Tag Archives: ins



logo

Recent Posts

Nov. 30, 2022

Coordinate frames and you

sander , , , , Leave a comment

It’s been a year since we last spoke. I thought that there couldn’t be a better topic to discuss than coordinate frames and rigid body transforms. </sarcasm>. In all seriousness, it’s a great concept to grasp solidly and hopefully will help you do the things that you do with inertial sensors more betterer.

Coordinate frames give you a reference of how you are moving through space. For a quick refresher, we understand that acceleration can be integrated to produce velocity, and velocity can be integrated to produce a relative position. This is all well and good, but if you do not have a proper understanding of which axis is forward, which axis is left, or which axis is up, integration of any of these data products will be wholly irrelevant.

Coordinate frames (based on our current understanding of the physical universe) are represented by three axis’, an X Y and Z. All of these axis are orthogonal to one another (simply meaning that they meet each other at 90 opposing degree angles). It can be somewhat difficult to understand which axis is which without a physical reference (a 3D object that can represent a coordinate frame that you can manipulate) or identification (a 2D image of a coordinate frame) to look at.

UNTIL NOW

…well, hopefully

Sidenote_00: I touched on this hand gesture in the last blog post, but it’s useful to go over again.

A useful thing to understand about coordinate frames is that most (used in evaluation of vehicle dynamics) follow a “right hand rule” convention. If you follow these steps below, you too can be like many physics / robotics researchers and make strange hand gestures when trying to intuitively comprehend coordinate frame rotations (which we will get to later).

– Make a fist with your right hand

– Stick your thumb out while still keeping the rest of your fingers in a fist

– Rotate your hand so that your thumb is pointing toward the sky

– Stick your pointer finger out so that it is pointing away from your body

– Stick your middle finger to your left

You have just created a coordinate frame. Following the right hand rule convention, your pointer finger is pointing forward and represents the +X axis, your middle finger is pointing toward the left and represents the +Y axis, and your thumb is pointing up and represents the +Z axis. You can represent any rotation of a right hand rule coordinate frame!

So now you’re probably thinking, “wow sander amazing”. I know. Just wait.

FLU, FRD, WAT?

The Bosch Motorsport MM5.10 IMU is relatively ubiquitous and used in many race cars. A non-motorsport version is even shipped as standard equipment in some of the most popular electric cars that are on the public roads today. The MM5.10 sensor coordinate frame is represented by the same funny hand gesture that I just made you do. This is referred to in short hand as a FLU (Forward, Left, Up) frame. Meaning that X+ is Forward, Y+ is Left, and Z+ is Up.

Sidenote_01: This FLU frame is described by the ISO 8855 standard. Mainly used in ground traveling vehicles.

The Obsidian INS and IMU products use a different coordinate frame from the MM5.10 IMU. We use a FRD (Forward, Right, Down) frame. Meaning that X+ is Forward, Y+ is Right and Z+ is Down.

Sidenote_02: This FRD frame is described by the ISO 1151 standard. Mainly used in aircraft.

You’re still holding your hand in the hand gesture that I asked you to just a little bit ago, right? If that’s the case, you can easily rotate your hand around the X axis (your pointer finger, in this case) 180 degrees, and voila, you went from holding your hand originally in an FLU frame and now you’re holding your hand in an FRD frame. Using this hand motion, it’s relatively easy to come up with the intuition that, if we want to compare data between an MM5.10 and an INS we will either need to mount the MM5.10 upside down, or mathematically rotate it after the fact.

SIdenote_03: WAT

Aligning frames unrealistically

In practice, it’s normal to see a vehicle outfitted with one or more inertial measurement sensors and sometimes they can be from different manufacturers that have different coordinate frame standards. Using the examples above, lets assume for a moment that we have a vehicle with an MM5.10 using a FLU convention and an INS using a FRD convention. In this case we will assume that the MM5.10 is mounted directly on top of the INS (to reduce the math to pure rotation only).

Sidenote_04: Three color coordinate frames are usually represented by X == red, Y == green, Z == blue

MM5.10 IMU in FLU frame mounted above Obsidian INS with FRD frame

The dumb (and / or) simple way to align these two reference frames is to take the data products (accel and angular velocity) of the MM5.10 in the Y and Z axis and multiply them by -1. This will very simply invert the data produced from the MM5.10 on those axis’ and you will have successfully “rotated” the FLU frame so that is now an FRD frame. For example, you can take the Y axis acceleration of the MM5.10 and multiply by -1 and that acceleration will line up with the raw Y axis acceleration of the INS.

The visualized frame would mathematically look like this below:

MM5.10 IMU rotated from FLU to FRD coordinate frame, mounted above Obsidian INS. Notice how the axes are now aligned.

After rotation the MM5.10 in to the same coordinate frame as the INS, the angular velocities (yaw rate, pitch rate, roll rate) would theoretically be the same, and the acceleration measurements would be almost the same (we’re not accounting for translations here to keep this post a little shorter). Easy peasy.

Which way is positive?

One of the most common questions I get about the INS / IMU has to do with direction of rotation. e.g. “Which direction is +10 degrees of pitch? Is the car pointing toward the sky or towards the ground?”. Thankfully, this is a fairly easy thing to intuitively solve when you use your very useful hand gesture that I described above.

Using your hand gesture, make a FLU coordinate frame to represent the MM5.10. This should make it such that your thumb is pointing toward the sky, your pointer finger is pointing forward, and your middle finger is pointing toward the left.

Maintaining that gesture, look at the tip of your thumb. If you rotate your hand around your thumb in a counterclockwise direction, this will be a positive rotation. The images below show a coordinate frame with a yaw value of 0, and a yaw value of +20 degrees.

A top down view of the MM5.10, looking in to the Z axis, where the X and Y axis are aligned with the grid below. This would represent a yaw value of 0.

A top down view of the MM5.10, looking in to the Z axis, where the X and Y axis are rotated with respect to the grid below. This would represent a yaw value of +20 degrees.

The same thing would apply for pitch and roll, as well. “Look” in to the positive axis (In an FLU / FRD frame, X for roll, and Y for pitch), and what ever direction is counterclockwise will be a positive rotation.

Aligning frames realistically

While I’d like to tell you that you can align coordinate frames by multiplying with -1, that’s not realistic. We exist in a very non binary world. Which is great for everyone. Imagine how hard it must be for computers that only know 1 and 0.

It’s not unrealistic to say that many race cars have less than perfect mounting of inertial sensors. In this example, let’s imagine a team trying to use an accelerometer in a dash logging display (MoTeC C1XX), or ECU (MoTeC M1XX) for driver analysis. It’s somewhat unlikely that the dash or ECU will be mounted so that the axes of the accelerometer are pointed exactly in the direction of motion that you are interested in (the vehicle’s natural coordinate frame). Maybe the dash / ECU is mounted “mostly straight” in the direction of travel, and / or “mostly perpendicular to gravity”. That doesn’t help us much if we’re trying to use this acceleration data for driver analysis.

Imagine that we are trying to use a MoTeC C127 dash that is angled at the driver like this:

Borrowed from Google image search via a Rennlist thread.

The MoTeC dash pictured above is angled such that the screen is visible to the driver. Being that the accelerometer in the MoTeC dash display is mounted to the PCB internal to the display itself, it’s reasonable to assume that the display being mounted at an angle will result in the accelerometer being mounted at an angle as well. In the interest of simplicity (as this post is already really long and we haven’t even done any math yet) we will assume that the MoTeC dash has zero roll, and zero pitch, with respect to the vehicle coordinate frame. The only thing we would notice in this case is that if the car is traveling exactly straight you may have acceleration in X and Y axes (assuming an FLU frame for the MoTeC dash itself and FLU for the vehicle frame).

MoTeC dash mounted with a -20 degree yaw angle with respect to the vehicle frame.

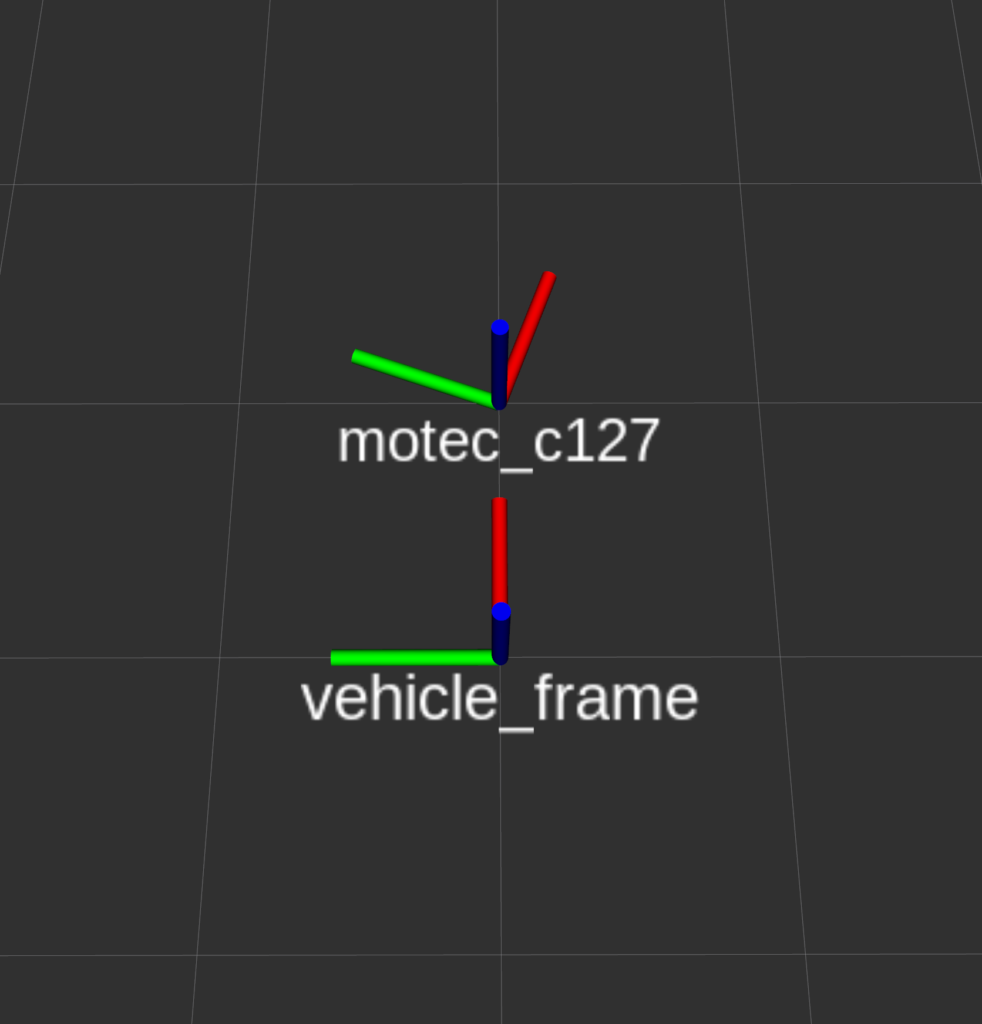
It’s relatively intuitive to see that if the vehicle is traveling exactly straight about the X axis (red in vehicle_frame), you will see acceleration in the X and Y axis in the MoTeC dash due to it’s mounting. Let’s work out how to mathematically rotate the accelerometer so that the data from the MoTeC dash is producing data as if it were mounted exactly straight (inline with the vehicle_frame).

I’ve made some simulated accelerometer data from a MoTeC dash if the vehicle was traveling straight at 9.81 m/s/s constant for 1 second (sampled at 10khz), mounted at some unknown yaw angle with respect to the vehicle_frame above.

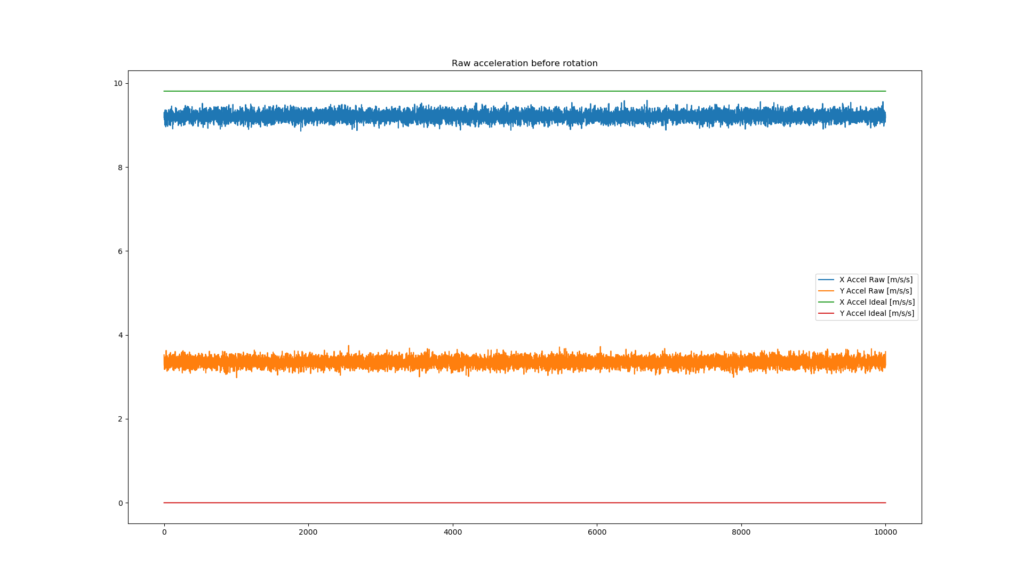
X, and Y acceleration in units of m/s/s (reminder 1G is equal to 9.81 m/s/s). X is in blue and Y is in orange.

We can use the following steps to rotate this data such that it aligns so that Y and Z are equal to roughly 0.0, while X is equal to 9.81 m/s/s.

codenote_00: python-pseudo-code

# step 1
# find the mean of each axis of acceleration
ax_mean = mean(raw_accel_x)
ay_mean = mean(raw_accel_y)

# step 2
# "guess" a suitable yaw angle of the motec_c127 with respect to the  vehicle_frame
guess_yaw_degree = -15.0

# step 3
# convert guess_yaw_degree to radians
guess_yaw_radians = guess_yaw_degree * pi / 180.0

# step 4
# find the resulting acceleration after rotation using 1D rotation formula
corrected_accel_x = ax_mean * cos(guess_yaw_radians) - ay_mean * sin(guess_yaw_radians)
corrected_accel_y = ax_mean * sin(guess_yaw_radians) + ay_mean * cos(guess_yaw_radians)

# step 5
# repeat steps 2 -> 5 until your corrected_accel_x is equal to roughly 9.81 and corrected_accel_y is equal to roughly 0.0

After you find your guess_yaw_radians channel, you can apply step 4 to all of your raw data and you should have a plot of data that looks like this!

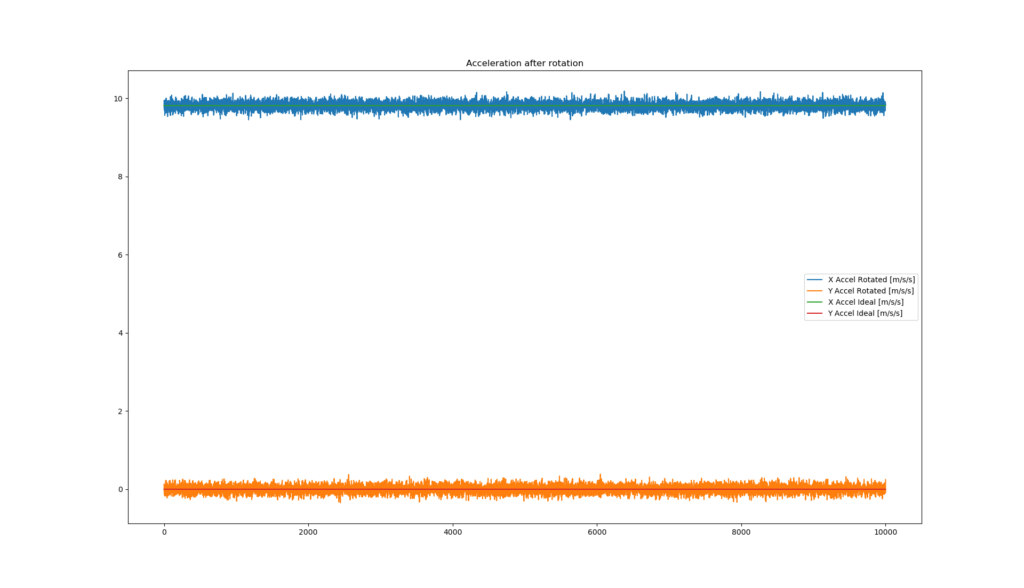
You can see here the X and Y acceleration after rotation. The X accel is roughly equal to 9.81 m/s/s and the Y accel is roughly equal to 0.0 m/s/s

So, you’ve done it. After that work you should have successfully applied a 1D rotation to acceleration data and after this equation, the data from your MoTeC dash should have been mathematically corrected such that the data would be the same if the MoTeC dash were mounted in the same orientation as the vehicle_frame.

BUT WAIT. THERE’S MORE.

Imagine that the MoTeC dash needs to be rotated in more than one axis (yaw only in the example above), what about a yaw rotation and a pitch rotation? Or worse, what about a yaw rotation, a pitch rotation, AND a roll rotation? What are we to do?

The answer is much more complicated and much more difficult to hand estimate using a “brute force” approach that I’ve described above. It is made simpler by applying the rotation in one operation using a rotation matrix as opposed to euler angles* (roll, pitch, yaw), which can be very annoying to deal with when doing 3D rotations.

Sidenote_05: Euler angles are actually often misrepresented as Tait-Bryan angles.

Fin

I do realize that I glossed over details of translation components in proper rigid body transforms. Honestly, I didn’t realize that it would be this difficult to convey this concept in a pseudo-math pseudo-code way that was easily digestible while still keeping with my normal style of posts. Thanks for sticking with it. If you made it this far, you’ve earned some relaxation

Aug. 03, 2021

INS or IMU? It depends.

sander , , , Leave a comment

It depends how long it takes you to do what ever you’re trying to do.

There. That’s the end of the article.

Just kidding.

A Terminology Tangent

First, you’re probably thinking, “Tangent? This guy hasn’t even started writing anything yet“.

Second, I probably should apologize for having two products, that look nearly identical, that have nearly the same name, targeted at different applications, and with wildly different price tags. I am trying to take the Ron Swanson approach to making products. I’d like to just call things what they are. No marketing, no flair, no sponsored product placements. So, anyway, let me take a second and remind you, my loyal readership, what these acronyms stand for:

INS stands for Inertial Navigation System. This is an industry term in robotics that, generally speaking, defines a system that is a GNSS receiver, accelerometer, gyroscope, barometer, and temperature sensor (among other sensors, sometimes) combined together with a complex sensor fusion algorithm to produce a single high-rate, high-accuracy 6DOF pose (and corresponding derivatives that we will talk about later in this post).

sidenote_1: 6DOF Pose stands for 6 Degree Of Freedom Pose. These 6 individual degrees of freedom are: Roll, Pitch, Yaw, X Position, Y Position, Z Position. When combined, they represent the position of the sensor in a 3D world.

IMU stands for Inertial Measurement Unit. This term is a bit more complicated. This is also an industry term (in robotics, and motorsport at the sub-pro level) that, generally speaking, defines way way too many different sensors, systems, and products.

In motorsport, an IMU is generally defined as a sensor that will give you acceleration, and angular velocity. It is generally a very basic raw sensor output with no sensor fusion or on-board math going on.

In robotics, an IMU is generally defined as an accelerometer, gyroscope, barometer, and temperature sensor combined together with a complex sensor fusion algorithm to produce high-rate / high-accuracy orientation (roll, pitch, yaw), acceleration, and angular velocity.

INS on the left, IMU on the right
The PPIHC Open Class champion that I was able to use as a test platform to benchmark some new INS and IMU beta features

So, as you can probably tell at this point, I’m following the terminology of the robotics world in naming these two products. The robotics definition of the INS is what the Obsidian Motorsport Group INS is. The same is true for the Obsidian Motorsport Group IMU.

Derivatives and Antiderivatives

I know, scary math word, but please relax. I’m going to do everything in my power to use intuitive examples to demonstrate some things about how the IMU (and to some extent, at a very basic level, the INS) derive some of their more interesting data products.

Derivatives are simply the representation of the change of something divided by the time it took to make that change. Antiderivatives (also referred to as Integration) are the opposite. Stay with me here, practical examples that are not your run of the mill “passenger on a train” physics examples are incoming…

Lets assume that you have a general purpose 3-axis accelerometer mounted in a vehicle, rigidly attached to the chassis, and the X-axis is pointed forward, the Y-axis is pointed left, and the Z-axis is pointed up.

sidenote_02: This accelerometer mounting mentioned above (and our INS / IMU…) follows a “Right-Hand Rule” convention. If you curl your right hand in to a fist and rotate it such that your thumb is up, and do the following:

  • Point your pointer finger forward
  • Point your middle finger toward the left
  • Point your thumb in the air

Your pointer finger will be the X-axis, your middle finger will be the Y-axis, and your thumb will be the Z-axis. No matter how you mount a “Right-Hand Rule” IMU, if you keep the finger-to-axis assignments the same, you’ll be able to envision what the coordinate frame looks like with your hand! Neat.

Using the coordinate reference frame mentioned above, when the vehicle travels forward, there will be positive acceleration present in the X-axis.

  • If you integrate the acceleration (using units of m/s/s) in the X-axis, you will get velocity (using units m/s) in the X-axis.
  • If you integrate the velocity (using units of m/s) in the X-axis, you will get position (using units of m) in the X-axis.

The picture below should illustrate that point well.

  • The blue trace at the top is a measure of longitudinal acceleration (forward + / backward – ) in units of m/s/s.
  • The green trace is a measure of longitudinal velocity in units of m/s. This is a result of integration of the blue trace.
  • The red trace is a measure of longitudinal position in units of m. This is a result of integration of the green trace.
Acceleration (top), Velocity (middle), Position (lower)

sidenote_04: It’s important to remember that there are a lot of factors that go in to creating an accurate acceleration measurement to do these integrations off of. You should absolutely try this on your own with whatever sensor you want to use, but be warned, It’s harder than you think to do this with a basic accelerometer.

So, now you know the relationship of acceleration, velocity, and position. I feel pretty strongly that this is an important concept to grasp to discuss the next part of this post…

Error

Now that we know how integration works, intuitively anyway, we can talk about the biggest issue with integration: error.

Accelerometers are not perfect instruments. Even the fanciest ones on the planet are prone to small error based on a multitude of factors (Namely temperature for the ones that normal civilians have access to). When we integrate acceleration to get velocity, any small error in acceleration, will propagate forward as an error in velocity. This is compounded when we integrate velocity to get position!

The picture below, should illustrate that point well. It is the same data as the trace above, but with some error introduced in the longitudinal acceleration measurement. Check out the position error at the end, it’s ~40m !

  • The purple trace at the top is “nearly” the same acceleration as the IMU Body Accel X [m/s/s] channel.
  • The purple trace in the middle is a result of integration of the purple acceleration measurement at the top. Notice the significant error (~4 m/s).
  • The purple trace at the bottom is a result of integration of the purple velocity trace in the middle. Notice the massive error (~40m).
The two acceleration channels don’t look that different, do they…

Our IMU goes through a factory calibration at the chip level, then a second calibration (at our office) to try to do our best to remove any errors that are introduced after installation (soldering). We spend a lot of time with this to try to give you acceleration data that is in blue, and not in purple.

In addition to our calibration processes, there are online algorithms that are running that are constantly (on the sensor itself) trying to estimate and correct any errors in the acceleration and gyroscope measurements to make sure that we’re providing you the best data possible. However, since those algorithms have no real understanding about how the vehicle is moving through the world (say, with a GNSS / GPS receiver like the INS…), these bias correction algorithms are only effective to a point. This “point” is about 30-45 seconds after the vehicle has left the starting line and the integration process has begun.

Do I need an INS or can I use an IMU? TELL ME, SANDER.

Okay, okay. I hear you.

The IMU is explicitly designed for standing start, ground vehicle, racing that lasts for less than 30-45 seconds.

The INS is explicitly designed for everything. Since the sensor has a GNSS / GPS receiver on board, the sensor can automatically mitigate biases that creep in over time to the accelerometer and gyroscope. It has no time bound.

The IMU will provide the following data products at up to 800hz:

  • Ground Speed*
  • Raw Acceleration (X, Y, Z)
  • Body Frame Acceleration (X, Y, Z)
  • Angular Velocity (X, Y, Z)
  • Orientation (Roll, Pitch, Yaw)

*The IMU will need to be sent a simple CAN message to tell it that the pass has started to generate Ground Speed. It’s easy to do, I promise.

The IMU will have the following features:

  • Adjustable baud rate (1mbps default, 500kbps, 250kbps)
  • Adjustable transmission rate (800hz, 400hz, 200hz, 100hz, 50hz, 25hz, 10hz).
  • Adjustable user tunable filters for acceleration / gyroscope data
  • Advanced Kalman filter tuning parameters

The sensor will be sold for $1750 and I will have a number in hand to sell in about 3-4 weeks. As always, if you have any questions, please email me at sander 4T obsidianeng d0t com

Now, you may be thinking, “Sander, you could have lead with that and I wouldn’t have had to read this stuff about derivatives, integration, and error propagation.”

You’re right. I could have.

Dec. 23, 2020

GPS? IMU? INS? What on Earth even is that?

sander , , Leave a comment

See what I did there?

I should start out by saying it’s been quite a while since I’ve written anything in a “blog” type format, so please be patient if I go off on a long tangent about something that’s powerfully uninteresting to you, my loyal readership.

Since my last post on this blog, I moved to California (San Francisco, specifically), got hit by yet another car while riding my bike, ate many delicious meals in San Francisco, had many successes with work, learned many hard lessons about living in a city, learned many more hard lessons about working with OE manufacturers on engineering projects, and (more relevant to this post) using / understanding / configuring / and making sense of Inertial GPS systems. Let’s go over some basics about the latter.

GPS / GNSS:

Many moons ago, I thought that when you placed a GNSS receiver / antenna on the roof of a race car, you could power it on, science would happen, and then it would tell you where on the earth you were. Magic.

I didn’t spend much time thinking about how it worked, because, well, it worked fine. It provided a nice visualization of where a car was on track. Fine. Great.

Over the past few years it has become increasingly obvious that it’s really important to understand how something works if you’re going to rely on the data it produces. A lot of the projects that I have been involved with over the past few years at some point rely on GNSS. It’s really important to know when to rely on it, when not to rely on it, and why.

sidenote_1: Sander, you keep writing “GNSS”, what does that even mean? “GNSS” stands for Global Navigation Satellite System. Some people often say “GPS” when they actually mean “GNSS”. You could plausibly argue that GNSS and GPS are interchangeable as ways to describe a system that can calculate where you are on the earth, but I felt it was worth mentioning that. GPS is actually a constellation (series of satellites in a specific orbit around the earth) of satellites that are owned and operated by the US Space Force. Yes, that Space Force. There are other constellations that are run by other countries such as “Galileo” (EU), “Beidou” (CN), “Glonass” (RU), “IRNSS” (India), “QZSS” (Japan). A GNSS system may use signals from satellites from one or more of these constellations to calculate your position on the globe. Neat right?

So, this begs the question: How do GNSS systems determine your position? How does it work? SANDER, TELL ME HOW SCIENCE HAPPENS!

sidenote_2: I’m going to do a super high level description of how things work, but if you’re interested in much more detail, you should really checkout this GPS Compendium (by u-Blox AG). It is a treasure trove of information about GNSS systems.

Basic things to know:

  • There are a number of satellites (in different constellations, run by different countries) orbiting the earth in a known trajectory / orbit.
  • Each satellite has an atomic clock on board to keep accurate time.
  • Atomic clocks are cool because they keep very accurate time for a very long time. (Not like your calculator wrist watch that you’re wearing right now. yes, you.)
  • Satellites regularly transmit their time so that GNSS receivers on the ground can receive this information.
  • If you take in a known position of the satellite, time from the satellite, you can use the speed of light as a constant to determine the distance from the GNSS receiver to the satellite.
  • You can determine a 3D position and time error with a minimum of 4 satellites. (Latitude, Longitude, Altitude, delta T error).
  • There are many sources of error that can cause accuracy issues (ionosphere time delay, multi-path signal errors, and other things outside the scope of this post)
  • The rate in which data is sent from these satellites will limit the rate at which we can calculate our position on the ground

That last bullet point is really the key issue here. Even very very expensive GNSS systems (NovAtel et. others) can not generate high frequency position measurements (lots of position updates every second) with just GNSS data alone. You need more data to help “fill in the gaps” between GNSS position updates. Well, how on earth would we “fill in the gaps”???

IMU (Inertial Measurement Unit):

IMU’s are generally understood to consist of a 3-axis accelerometer and a 3-axis gyroscope. What even is that? Let’s start with the accelerometer.

IMU (Accelerometer):

Like the name implies, the accelerometer measures acceleration. Now, you may be thinking, “Wow, Sander, you’re blowing my mind right now”. Or, maybe you’re not thinking that, hard to say.

I know that’s inherently obvious based on the name, but another way to think about acceleration measurement is that there is always acceleration to be measured (at least on our planet) by way of gravity. If you set a 3-axis accelerometer on a flat table, you will notice that the axis that is pointing up will report approximately 9.81 meters / second / second of “acceleration”. This is the measurement of gravity acting upon the table to keep it from floating away.

What can we do with an accelerometer beyond all of the well meaning, but painfully over simplified, statements about “my car pulled 3g’s off the line” or “I saw 2.5 lat G in T5 at Summit Point”? We can use calculus! From acceleration we can determine velocity doing a single integration, and we can determine relative position doing a double integration!

sidenote_3: I’m intentionally skipping an entire large chunk of explanation about removing gravity from acceleration measurements to actually get something useful from them and before integration to achieve velocity measurements, and entirely skipping bias calculation / error sources, for now.

This example shows live data from our INS (Body Accel X [m/s/s] and Body Velocity 2D [mph]). It also shows that you can integrate the Body Accel X [m/s/s] data and return velocity in the X axis ( t1_vel_x_integration [mph] ), and even distance traveled ( t1_dist_traveled [ft] )!

sidenote_4: Live distance traveled channels are being prototyped now and will be added to the sensor firmware later in 2021.

IMU (Gyroscope):

Like the name implies, the gyroscope measures gyroation. (Sorry, this is wildly incorrect, I just thought it would be funny at the time of writing relative to my previous bit about accelerometers measuring acceleration).

Gyroscopes measure the angular velocity about an axis. A simple way to think about this is if you placed a gyroscope on your hipster friends turntable (ya know, for vinyl records), and turned it on, the axis that is pointing straight up will probably indicate ~200 deg/second (33.3 RPM for 12″ records). This is simply measuring the speed at which the turntable is spinning.

What can we do with a gyroscope beyond making your friend with the turntable nervous by telling him it’s actually spinning at 198 deg/second as opposed to the 199.7999999999999999 deg/second it should be? You guessed it, more calculus! From angular rate we can determine the relative angles (more simply put, relative roll, pitch, and yaw) doing a single integration!

sidenote_5: It’s important to remember that in a rigid body (something that doesn’t flex or distort about the axis in which you’re measuring), the angular velocity (and resulting angle after integration) will be the same no matter where you place the gyroscope on the rigid body. Another way to think about this is simply that if you have a motorcycle that does a wheelie, no matter where you mount a gyroscope, the resulting pitch angle after integrating the pitch rate will be the same. 

This example shows live data from our INS on all channels.

sidenote_6: The pure_relative_pitch [deg] channel has a simple subtraction function to compensate for the mounting of the sensor in the vehicle. The live pitch measurement from the sensor will be absolute pitch (relative to gravity vector).

IMU (Error):

IMU’s are great because they can be light and small and provide very high rate data (1khz +), but it is also important to remember that they can be subject to long term integration error. These errors are omnipresent in in all IMU’s but especially ones that us common folk (read: not military) are allowed to buy.

Cheap IMU’s (less than a $10,000.00 or so) are usually Micro Electrical Mechanical System (MEMS) based units. They’re great because they’re small, cheap, light weight, and low power. But they are prone to massive error (usually mainly based around temperature, but there are other sources of error, too) if doing numerical integration over long time windows.

sidenote_7: “…long time windows” are definitely relative. Many consumer grade sensors (cheap) can even start showing integration error in seconds! On the flip side, many tactical grade (usually military only and > $10,000) will measure their integration error in hours)

These errors are tough to calibrate out, and are better addressed if you have another reference to compare your velocity and position to, periodically.

INS (Inertial Navigation System):

Here are some things we now understand:

  • GNSS systems can be highly accurate, but the rate at which they can provide position updates is relatively slow.
  • IMU’s can provide very fast measurements from which you can determine position, velocity, and orientation. However, their accuracy can become quite poor very quickly when doing single (or double) integrations.

An Inertial Navigation System (INS), combines these two sensors and uses the global accuracy of a GNSS system and the speed of an IMU! These INS systems use some derivative of a Kalman Filter (non-linear Extended or Unscented) to combine these sensor inputs perform what is sometimes called “Sensor Fusion” to generate one smooth cohesive output.

sidenote_8: Kalman Filters are a constant source of interest and wonder, however I think explaining how they work is outside of the scope of this blog post.

What is the point of this wall of text:

Well, I have put together an Inertial GPS system that I would like to sell. I am simply calling an INS. It uses a tried and true Extended Kalman Filter that is very robust and platform (or motion model) agnostic (car, motorcycle, plane, rally-car (read: plane)). I have tried really hard to make integrating this sensor as easy as is humanly possible to any modern, high-end data analysis / control system.

Here are the features:

  • 400Hz 32-bit Position (Latitude, Longitude, Altitude)
  • 400Hz 32-bit Velocity (Body X, Body Y, Body Z, and 2D Speed)
  • 400Hz 32-bit Body Frame Acceleration (Gravity Removed) (X, Y, Z) with online acceleration bias compensation
  • 400Hz 32-bit Angular Rate (X, Y, Z) with online gyro bias compensation
  • 400Hz 16-bit Orientation (Roll, Pitch, Yaw (Degrees))
  • 100Hz “MoTeC GPS” simulation option for integration with MoTeC M1 ECU applications with locked firmware (GT-R, Lamborghini, etc…)
  • CAN (1mbps) Output
  • Extensive integration support (MoTeC Dash Config, MoTeC M1 Build Project Module, DBC file)
  • CNC aluminum enclosure with Deutsch ASL connection and optional IP68 sealing
  • Custom firmware available for customer specific addressing, precision, transmit rates, conversions, units, additional on-board math channels, etc…

On the www.obsidianeng.com/downloads page you will find manuals, DBC files, MoTeC dash configuration files, and MoTeC M1 Build Modules.

The sensors will be available for purchase in Q1 2021. The cost will be $4500.00. Please shoot me an email (sander at_sign obsidianeng.com) with more questions.